Asymptote Calculator

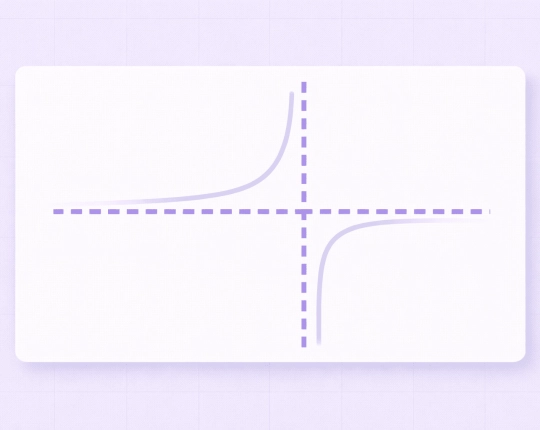
How Asymptotes Describe Function Behavior Near Infinity

An asymptote is a line that a graph approaches but never fully reaches. It describes the behavior of a function near undefined values or as the variable moves toward infinity.

Asymptotes help mathematicians understand long-term function behavior, discontinuities, and unbounded growth patterns.

For example, as \( x \to \infty \), a function may approach a constant value such as \( y = 0 \), forming a horizontal asymptote.

They are fundamental in algebra, calculus, engineering, and physics modeling.

A modern asymptote calculator evaluates these behaviors automatically using algebraic simplification and limit analysis.

Types of Asymptotes

Functions may contain three primary asymptote types.

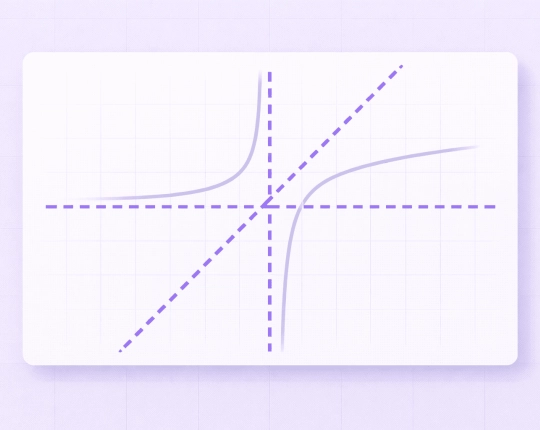
• Vertical asymptotes
  These occur when a function becomes undefined, typically when the denominator equals \( 0 \). As \( x \) approaches that value, the function increases or decreases toward \( \infty \) or \( -\infty \).
• Horizontal asymptotes
  Horizontal asymptotes describe the behavior of a function as \( x \to \infty \) or \( x \to -\infty \). They reveal long-term output trends.
• Oblique (slant) asymptotes
  When a function does not level off horizontally, it may approach a diagonal line instead. These often appear in rational functions where the numerator degree exceeds the denominator degree by \( 1 \).

Vertical Asymptotes Explained

Vertical asymptotes form when division by zero occurs in rational expressions.

Example:

\( f(x) = \frac{1}{x – 2} \)

The denominator equals zero at \( x = 2 \), creating a vertical asymptote.

Near this value, the function outputs increase or decrease infinitely. A limit calculator with steps often evaluates left-hand and right-hand limits to confirm asymptotic behavior.

Horizontal Asymptotes and Limits

Horizontal asymptotes depend on how the numerator and denominator degrees compare.

Rules include:

• If numerator degree < denominator → asymptote at \( y = 0 \)
• If degrees are equal → ratio of leading coefficients
• If numerator degree > denominator → no horizontal asymptote

Oblique Asymptotes

Oblique asymptotes appear when the numerator degree exceeds the denominator by one.

To find them, polynomial division is required. The quotient (excluding the remainder) forms the slant asymptote equation.

This process mirrors techniques used in algebraic division and may involve derivative or growth analysis when studying curve behavior near the asymptote.

Asymptotes in Exponential Functions

Not all asymptotes arise from rational expressions. Exponential functions also exhibit asymptotic behavior.

Example:

\( f(x) = e^x \)

When \( x \) tends to negative infinity, the function tends to be equal to \( y = 0 \) but never achieves it.

The modeling of such behavior may involve calculators such as an exponential function calculator, a tool that can be used to model growth and decay curves, as well as the positioning of the asymptotes.

Role of Derivatives in Asymptote Analysis

While limits define asymptotes, derivatives explain how functions approach them.

A derivative calculator can determine slope behavior near asymptotes, revealing whether curves approach steeply, gradually, or with inflection changes.

This insight becomes valuable in curve sketching, optimization problems, and motion modeling.

Step-by-Step Example

Consider:

\( f(x) = \frac{2x + 3}{x – 1} \)

Step 1: Find the vertical asymptote

Denominator equals zero at \( x = 1 \) → vertical asymptote.

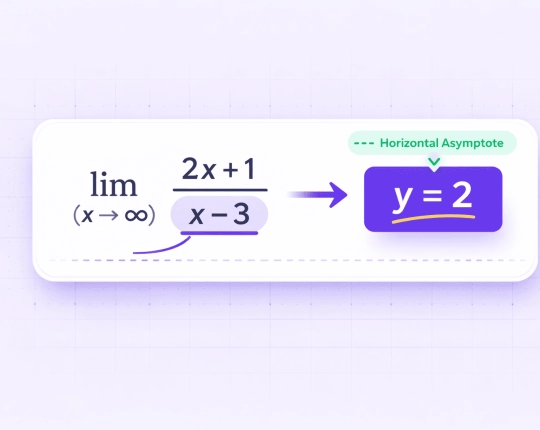
Step 2: Check horizontal asymptote

Degrees are equal → ratio of leading coefficients \( \frac{2}{1} \) → \( y = 2 \).

Step 3: Confirm with limits

Evaluating limits near infinity confirms horizontal behavior.

An asymptote calculator performs all steps instantly while displaying supporting logic.

Why Asymptotes Matter

Asymptotes reveal hidden structure in function graphs.

They help:

• Predict long-term growth
• Identify discontinuities
• Model physical limits
• Analyze rational equations
• Understand infinite behavior

In economics, the asymptote model shows diminishing returns.

In physics, they describe terminal velocity or wave decay.

In engineering, they help evaluate system limits.

Common Mistakes When Finding Asymptotes

Students often make recurring analytical errors:

• Ignoring removable discontinuities
  Factored terms may cancel, eliminating false asymptotes.
• Misreading degree comparisons
  Horizontal asymptotes depend strictly on polynomial degrees.
• Skipping limit verification
  Not all infinite behaviors produce asymptotes.
• Confusing slant and curved growth
  Not every non-horizontal trend forms an oblique asymptote.

Automation through an asymptote calculator prevents these conceptual mistakes.

How the Asymptote Calculator Works

The calculator processes the function in structured stages.

First, it simplifies the equation algebraically.

Next, it evaluates denominator zeros to detect vertical asymptotes.

Then, it compares polynomial degrees for horizontal or oblique cases.

An AI math solver layer can interpret every step in natural language when advanced explanation is turned on, leading to better conceptual understanding.