Logarithm Calculator

What Is a Logarithm?

One of the most important questions is answered by a logarithm:

What is the power to be lifted to give a certain number?

Example:
\( \log_{10}(100) = 2 \)
Because \( 10^2 = 100 \).

Logarithms are used to reverse exponentiation. While exponents grow numbers, logs determine the exponent that created them. A log calculator automates this reversal instantly.

Applications of Logarithms

• Algebra
• Calculus
• Statistics
• Finance
• Computer science

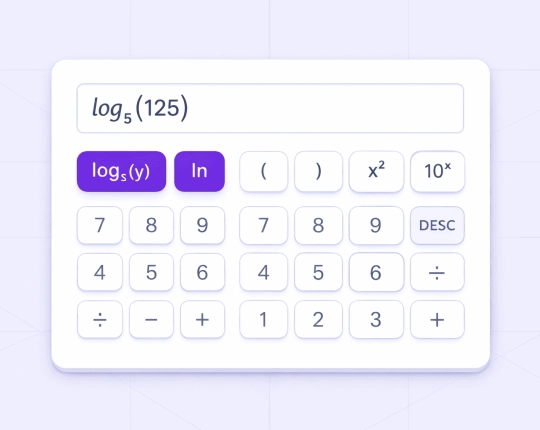
Common Types of Logarithms

Common logarithm (base \( 10 \))
Written as \( \log(x) \). Widely used in science and engineering.

Natural logarithm (base \( e \))
Written as \( \ln(x) \). Essential in calculus and exponential growth modeling.

Custom base logarithm
Written as \( \log_{b}(x) \). Used in specialized equations and computer algorithms.

A log calculator evaluates all these types automatically.

Logarithmic Rules and Properties

Logarithms follow structured algebraic rules:

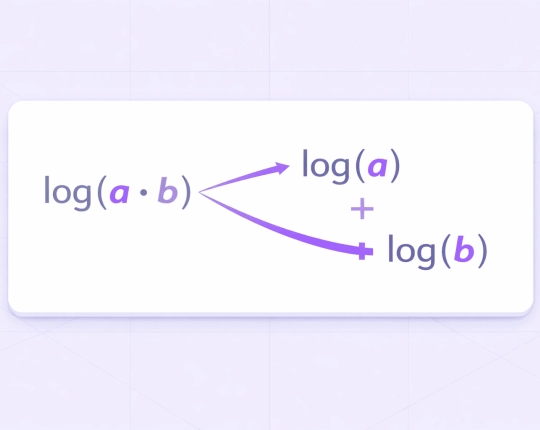
• Product rule
  \( \log(a \times b) = \log(a) + \log(b) \)
• Quotient rule
  \( \log\left(\frac{a}{b}\right) = \log(a) – \log(b) \)
• Power rule
  \( \log(a^n) = n \cdot \log(a) \)
• Change of base rule
  \( \log_{b}(x) = \frac{\log(x)}{\log(b)} \)

The calculator applies these properties step by step to simplify complex expressions.

Converting Between Logs and Exponents

All logarithmic equations can be converted into exponential forms.

Example:
\( \log_{2}(8) = 3 \)

Equivalent exponential form:
\( 2^3 = 8 \)

The knowledge of this relationship is useful when working out exponential equations or when analyzing growth models. These conversions are automatically performed with the help of a log calculator.

Solving Logarithmic Equations

Logarithmic equations must first be put into a form with the logarithmic expression isolated, and then converted to exponential form.

Example:
\( \log(x) = 3 \)

Rewrite as:
\( 10^3 = x \rightarrow x = 1000 \)

More complicated equations might require combining logarithms, applying power rules, or simplifying both sides of the equation.

In calculus contexts, solving such equations often integrates with tools like a free derivative calculator when logarithms appear in rate-of-change problems.

Exponential Growth and Logarithms

Logarithms are closely associated with exponential functions.

They appear in:

• Population growth models
• Compound interest calculations
• Radioactive decay
• Algorithm complexity

When exponential curves are analyzed graphically, asymptotic behavior may emerge. In such cases, an asymptotes calculator helps identify long-term boundaries of logarithmic or exponential graphs.

Natural Logarithms in Calculus

Natural logarithms \( \ln(x) \) play a central role in calculus.

They simplify derivatives and integrals that involve exponential functions.

Examples:
\( \frac{d}{dx} \ln(x) = \frac{1}{x} \)
\( \int \frac{1}{x} \, dx = \ln|x| + C \)

Owing to this relationship, logarithmic analysis is often used together with an integral calculator when solving problems involving area or accumulation.

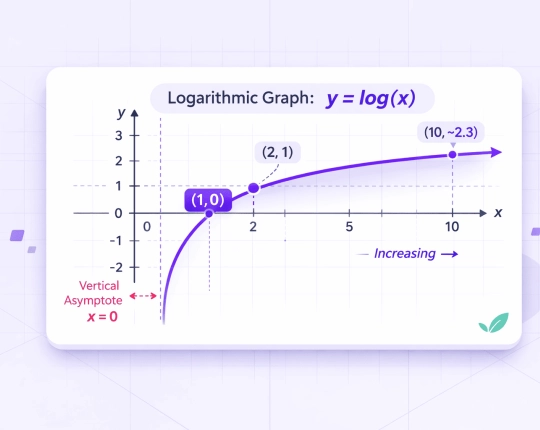
Graph Behavior of Log Functions

Logarithmic graphs share consistent characteristics:

• They pass through \( (1, 0) \).
• They grow slowly compared to exponential functions.
• They never touch the \( y \)-axis.
• The vertical axis \( x = 0 \) is a vertical asymptote because \( \log(0) \) is undefined.

Sample Log Calculation With Clear Steps

Evaluate:
\( \log_{2}(32) \)

Step 1: Convert to exponential form
\( 2^x = 32 \)

Step 2: Identify the exponent
\( 2^5 = 32 \)

Step 3: Final result
\( \log_{2}(32) = 5 \)

A log calculator performs this instantly while explaining each transformation.

Practical Applications of Logarithms

Logarithms appear across many industries:

• Finance
  Used in compound interest and investment growth models involving exponential functions such as \( A = P(1 + r)^t \).
• Data science
  Log scaling such as \( \log(x) \) improves data visualization and handles large-value distributions.
• Engineering
  Signal strength and decibel calculations rely on logarithmic formulas like \( 10 \log_{10}\left(\frac{P_1}{P_2}\right) \).
• Medicine
  pH levels use logarithmic concentration scales defined by \( \text{pH} = -\log_{10}[H^+] \).
• Computer science
  Algorithm complexity often follows patterns such as \( \log(n) \), especially in binary search and divide-and-conquer methods.

Automation through a log calculator ensures precision and efficiency in these domains.

Common Mistakes When Working With Logs

Several recurring issues appear in manual calculations:

• Ignoring log rules
  Failing to correctly apply properties such as \( \log(a \times b) = \log(a) + \log(b) \) or \( \log\left(\frac{a}{b}\right) = \log(a) – \log(b) \).
• Wrong base interpretation
  Confusing natural logarithms \( \ln(x) \) with common logarithms \( \log(x) \) (base \( 10 \)).
• Invalid inputs
  Logarithms are undefined for negative numbers or zero in the real number system, meaning expressions like \( \log(-5) \) or \( \log(0) \) are not valid.
• Conversion errors
  Miswriting exponential equivalents, such as incorrectly converting \( \log_{b}(x) = y \) into exponential form \( b^y = x \), leads to incorrect solutions.

A structured log calculator eliminates these risks through rule-based processing.

From Expression Input to Final Log Solution

The calculator performs both symbolic and numerical evaluation of logarithmic expressions.

• First, it identifies the type of logarithm and its base, such as \( \log_{10}(x) \), \( \ln(x) \), or \( \log_{b}(x) \).
• Next, it applies simplification rules including the product, quotient, and power properties like \( \log(a^n) = n \log(a) \).
• When solving equations, it transforms logarithmic equations such as \( \log(x) = 3 \) into exponential form \( 10^3 = x \).

This multi-level processing ensures computational accuracy while reinforcing clear mathematical concepts.