Simplify Calculator

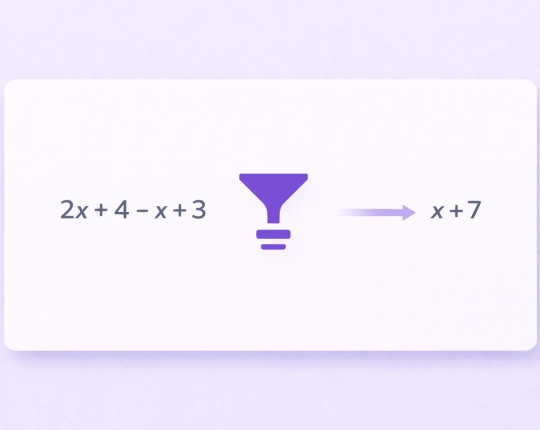
What Does It Mean to Simplify an Expression?

The simplification of an expression is the process of rewriting an expression in the simplest and most readable form possible without alteration of its value. This can be done by grouping similar words and phrases, fractions, number factoring, and rationalization of denominations.

For example:

• 2x + 3x simplifies to 5x
• 6/12 simplifies to 1/2
• √50 simplifies to 5√2

The aim is always directness and effectiveness. An uncomplicated outcome is more accessible to interpretation, further computation, or implementation in equations.

Types of Problems a Simplify Calculator Solves

A calculator of the modern era has a broad variety of mathematical operations:

• Fractions
  It decomposes fractions to the lowest terms by identifying shared factors. In cases of necessity, it is in collaboration with a free fraction calculator, which is used to convert improper fractions or mixed numbers.
• Algebraic expressions
  Coefficients and variables are simplified to a poly-form.
• Radicals
  Square roots and higher radicals decrease the extracting of perfect powers.
• Exponents
  The rules of operations of powers include multiplication, division, and negative exponents.
• Complex expressions
  Multi-step expressions simplify by using the order of operations and factor cancellation.

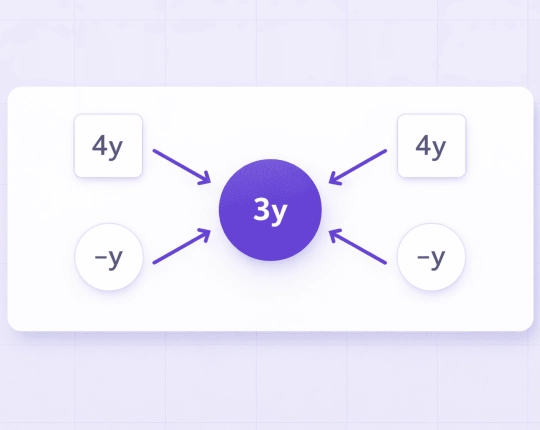
Simplifying Fractions

One of the most typical use cases is that of fraction simplification. The calculator determines the greatest common divisor (GCD) shared by both the numerator and denominator. It then divides the numerator and denominator by the same value to reduce the fraction to its lowest terms.

Example:
18/24 → divide by 6 → 3/4

In cases where the variables or a given polynomial are present in fractions, the calculator factors then reduces the parts. This is related directly to techniques in a factoring calculator, particularly with algebraic fractions.

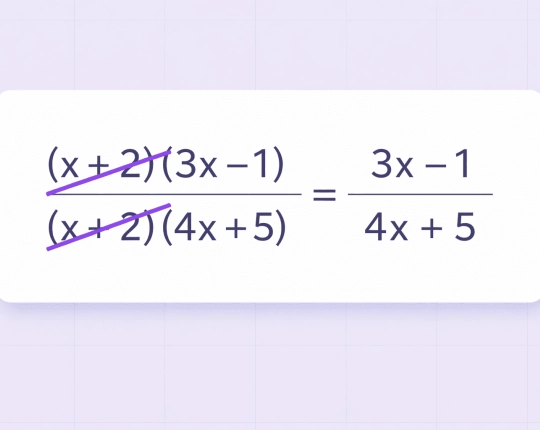
Simplifying Algebraic Expressions

Algebraic simplification focuses on combining like terms and reducing polynomial structures.

Example:
4x + 7x − 2x = 9x

When expressions grow more complex, factoring becomes essential. The calculator may extract common factors or apply identities such as:

• Difference of squares
• Perfect square trinomials
• Quadratic factorization

Radicals and Roots Simplification

Radicals simplify by extracting perfect squares or higher powers.

Example:
\( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \)

The calculator automatically detects factorable components inside the radical. This avoids manual trial-and-error and ensures correct reduction.

Radical simplification often appears in geometry, physics, and engineering formulas where exact values matter more than decimals.

Exponents and Powers

Expressions with exponents follow strict mathematical laws:

• \( a^m \times a^n = a^{m+n} \)
• \( a^m \div a^n = a^{m-n} \)
• \( (a^m)^n = a^{mn} \)

The simplify calculator applies these automatically, reducing expressions into compact exponential form.

This becomes especially useful in calculus, scientific notation, and algebraic modeling.

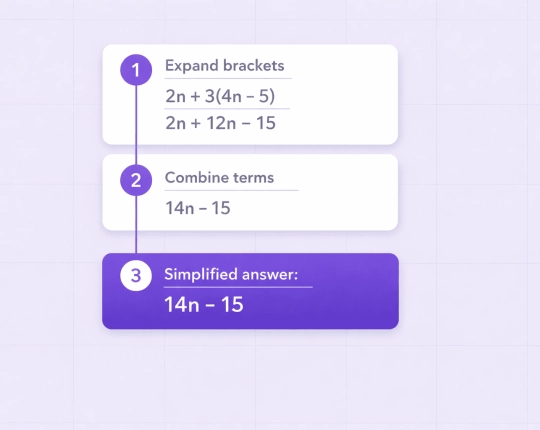
Order of Operations in Simplification

Complex expressions require structured evaluation using PEMDAS/BODMAS rules:

• Parentheses
• Exponents
• Multiplication and division
• Addition and subtraction

The calculator follows this hierarchy precisely. It may also integrate polynomial reduction, fraction simplification, or factoring at intermediate steps.

When division appears inside algebraic simplification, logic similar to a long division calculator may apply, particularly for polynomial division.

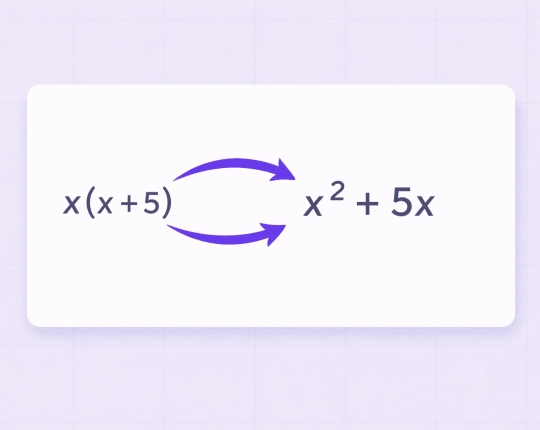
AI-Enhanced Simplification

Modern tools extend beyond static math engines. An AI math solver can interpret expressions written in natural input, scanned text, or complex notation.

AI support enables:

• Expression recognition
• Step explanations
• Method comparisons
• Error detection

By combining symbolic algebra with AI reasoning, simplification becomes both computational and educational.

Practical Applications of Simplification

Simplification is not limited to classroom exercises. It appears in:

• Equation solving
  Simplified expressions make isolating variables easier.
• Engineering formulas
  Reduced equations improve readability and reduce substitution errors.
• Finance calculations
  Interest formulas and ratios often simplify before evaluation.
• Physics problems
  Distance, velocity, and force equations rely on algebraic reduction.
• Data modeling
  Statistical and exponential expressions require simplification before interpretation.

Common Mistakes When Simplifying

Students and professionals alike make recurring simplification errors:

• Incorrect factor cancellation
  Cancelling terms that are added rather than multiplied leads to wrong results.
• Sign errors
  Negative values often flip during factoring or distribution.
• Partial simplification
  Stopping before full reduction leaves expressions unnecessarily complex.
• Exponent misrules
  Confusing multiplication and power rules produces invalid answers.

A structured simplify calculator prevents these issues by applying validated algebraic logic.

How the Simplify Calculator Works

The calculator processes expressions through symbolic algebra systems. It first parses the structure of the input, identifying numbers, variables, operators, and grouping symbols.

Next, it applies simplification layers:

• Combine like terms
• Reduce fractions
• Factor expressions
• Simplify radicals
• Apply exponent laws