What Is a Series?

A series is the sum of the terms of a sequence. While a sequence enumerates values, a series is about their sum.

As an illustration, 1 + 2 + 3 + 4 can be considered a series derived from natural numbers.

The differences of a series may be fixed, or it may have a fixed ratio, or it can be defined by some other rule. Moreover, the series can be finite or infinitely long. The way to the right calculation depends on recognizing the structure.

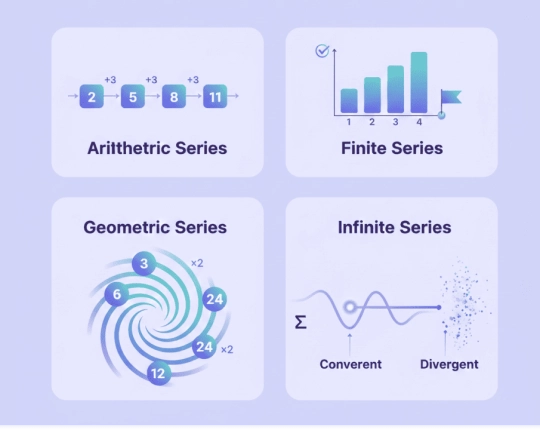
Types of Series

Arithmetic series

Arithmetic series follows a constant difference between one term and another. The first term, the last term and the number of terms are normally required to determine its sum.

Geometric series

A geometric series forms when each term is multiplied by a constant ratio. This type often appears in finance and compound growth problems.

Finite and infinite series

The beginning and ending of a finite series are clear.
A series is infinite, i.e., has no endpoint, and may or may not approach a limit.

Divergent and convergent series

A series that is infinite converges when it is having a constant number of sums. It is not linear as the total increases indefinitely. In the case of geometric series, convergence is determined by the ratio absolute value.

Smith, Fromberg, and Young (2018) provide a guide on how to determine the sum of a series.

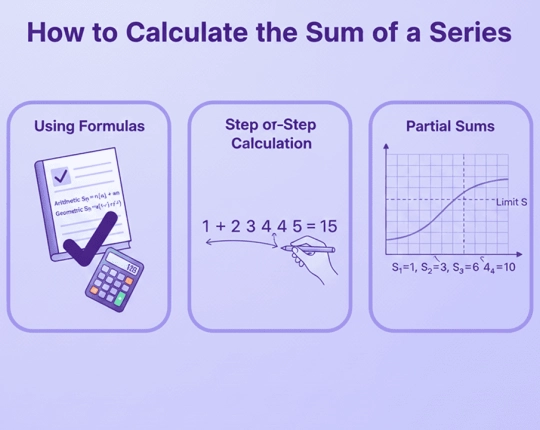
How to Calculate the Sum of a Series

Using formulas

Formulas work best when the series pattern is clear. Arithmetic and geometric series each use different formulas, based on known terms and ratios.

Step-by-step calculation

For short series or unclear patterns, listing and adding terms directly helps verify results and understand the structure.

Partial sums

With partial sums you can examine the behavior of a long or infinite series locally before making a final decision about convergence.

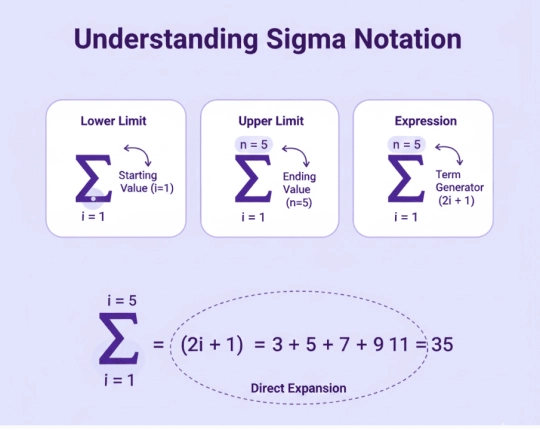
Understanding Sigma Notation

Sigma notation (Σ) is a concise means of representing a summation. It consists of:

• a lower limit (starting value),
• an upper limit,
• an expression that generates each term.

The index under the sigma changes with each step, while constants remain fixed. Once these elements are clear, the series can be evaluated using formulas or direct expansion.

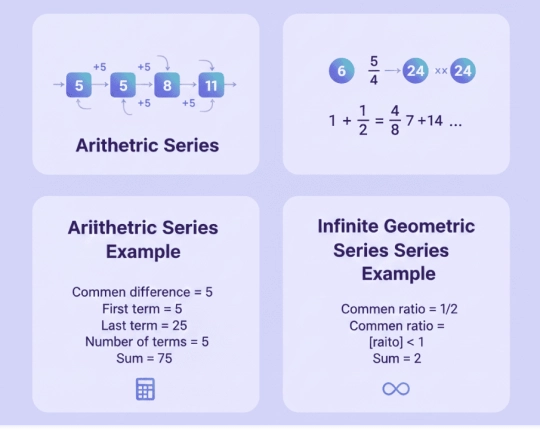
Step-by-Step Series Examples

Arithmetic series example

5 + 10 + 15 + 20 + 25

The common difference is 5.

First term = 5, last term = 25, number of terms = 5.

The sum equals 75.

Infinite geometric series example

1 + 1/2 + 1/4 + 1/8 + …

The probability ratio is 1/2 and its absolute value is less than one.

The series are all equal, and the total is 2.

Common Mistakes With Series

The most common mistake is the inappropriate formula of the series of the type. Arithmetic and geometric patterns might seem to be similar.

A second problem is counting terms incorrectly, particularly in sigma notation when the index is not initially 1. Sequences can also be mixed up with series although one lists and the other adds.

Checking convergence before applying infinite formulas helps avoid incorrect results.

How the Sum of Series Calculator Works

The calculator analyzes the input expression and identifies the series type automatically.
For finite cases, it applies the correct formula using the required number of terms.
For infinite series, it checks convergence conditions and reports whether the sum exists.

Because every step is shown, the tool supports both learning and result verification without hidden shortcuts.